正規化（normalization）とは

データベース内のデータ項目の重複と冗長性を排除し、データの独立性を維持するために行うグループ化のことです。一般的にデータベースの論理設計時に行う設計手法です。

 

データベース設計上の注意点

データベースを設計する場合、以下の点に注意する必要があります。

データ重複の排除：データ相互間の整合性が維持され、更新や削除を容易に行えるデータ構造であること

データ冗長性の排除：異句同義語・同音異義語を排除し、データ入力や加工、分析の不具合や混乱をさけるデータ構造であること

データ独立性の維持：データ項目を標準化し、設計・開発時の不具合や混乱をさけるデータ構造であること

 

DOAでも述べた通り、以下の点を意識したデータ構造であるということです。

１．データは一か所で登録される。

２．複数箇所で使用される。

これらを実現するために正規化を行います。

 

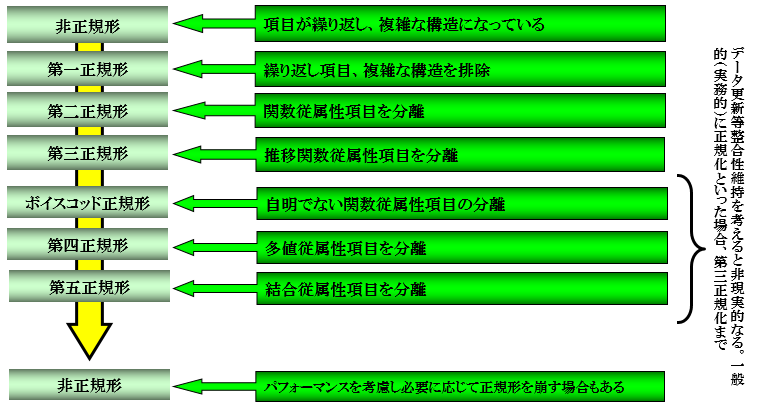
正規形とは

正規化では非正規形のデータ構造状態を段階的に正規形に分解していきます。非正規な状態とは、項目が繰り返し、複雑な構造になっている状態のことです。

 

 

正規形とはリレーショナルデータベース（RDB)操作のために有効な性質を持った一定の形ということです。

 

第1正規形 (first normal form：1NF)

繰り返し項目、複雑な構造を排除した状態のことです。ここで繰り返し項目を分離するという解釈もありますが、分離は第2正規形以降で行います。

 

第2正規形 (second normal form：2NF)

部分関数従属性項目を分離します。後述の関数従属性のうち、部分関数従属性項目（主キーの一部の項目の関係性と理解して大丈夫です）を分離します

 

第3正規形 (third normal form：3NF)

推移関数従属性項目を分離します。後述の関数従属性のうち、推移関数従属性項目（主キー以外の項目の関係性と理解して大丈夫です）を分離します

 

ボイス・コッド正規形 (Boyce/Codd normal form：BCNF)

自明でない関数従属性項目の分離します。実務では使用しませんので割愛します

 

第4正規形 (fourth normal form：4NF)

多値従属性項目を分離します。実務では使用しませんので割愛します

 

第5正規形 (fifth normal form：5NF)

結合従属性項目を分離します。実務では使用しませんので割愛します

 

関数従属性

正規化を理解するには、関数従属性を理解する必要があります。

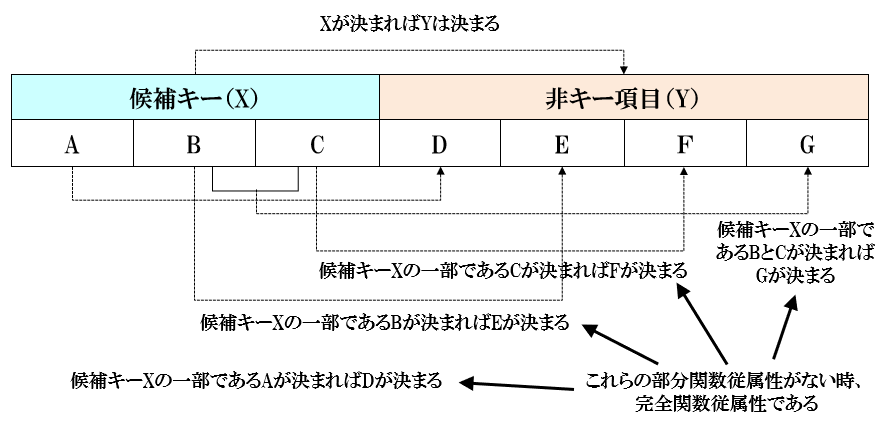
関数従属性とは、関係（リレーション）の中で、Xの値が決まるとYの値が決まることです。

関数従属性には、以下のものがあります。

完全関数従属性・・・X→YかつXのどんな真部分集合Xに対してもX→Yを満たさない時、完全関数従属性といいます。

部分関数従属性・・・候補キーの真部分集合に対する関数従属性を部分関数従属性といいます。

推移関数従属性・・・X→YかつY→Zであるならば、X→Zである時、推移的関数従属性といいます。

自明な関数従属性・・集合Yが集合Xの部分集合ならば、X→Yの関数従属性が成り立つ時、自明な関数従属性といいます。

多値従属性・・・・・Xの値が決まると、Yの値の集合が一意に決まることを多値従属性といいます。

結合従属性・・・・・分解によって得られる表が結合によって、もとの表に戻ることが可能であることを結合従属性といいます。

完全関数従属性

 

推移関数従属性

情報無損失分解

実務レベルで正規化と言った場合は、第３正規形までを言います。つまり、行（タプル）挿入・変更・削除時異常及び情報無損失分解の両方を実現できるのが第３正規形だからです。行（タプル）挿入・変更・削除時異常とは、その名のとおりデータ操作の不整合が起こることです。情報無損失分解とは自然結合しても元の関係（リレーション）に戻らない分解のことです。最後に非正規形戻し（正規化崩しとも言う）を行う場合があります。これは、実務レベルで行（タプル）挿入・変更・削除異常と処理効率のトレードオフになります。つまり、正規化した場合、レスポンス（ソフトウェア品質）が悪くなる等の問題を解決する場合に行います。但し、非正規形戻しは、必ず第３正規形まで正規化した後に行います。