正規化を理解するには、関数従属性を理解する必要があります。関数従属性とは、関係(リレーション)の中で、Xの値が決まるとYの値が決まることです。正規化に関係する従属性は以下の通りです。第三正規形に必要な関数従属性は、完全関数従属性、部分関数従属性、推移関数従属性までです。
完全関数従属性
X → Y かつ Xのどんな真部分集合X’に対してもX’→ Yを満たさない
部分関数従属性
候補キーの真部分集合に対する関数従属性を部分関数従属性という
推移関数従属性
X → Y かつ Y → Z であるならば、X → Zである
自明な関数従属性
集合Yが集合Xの部分集合ならばX → Y の関数従属性が成り立つ
多値従属性
Xの値が決まると、Yの値の集合が一意に決まることを多値従属性という
結合従属性
分解によって得られる表が結合によって、もとの表に戻ることが可能であることを結合従属性という
完全関数従属性と部分関数従属性の意味
以下の図は完全関数従属性と部分関数従属性の関係を表した図です
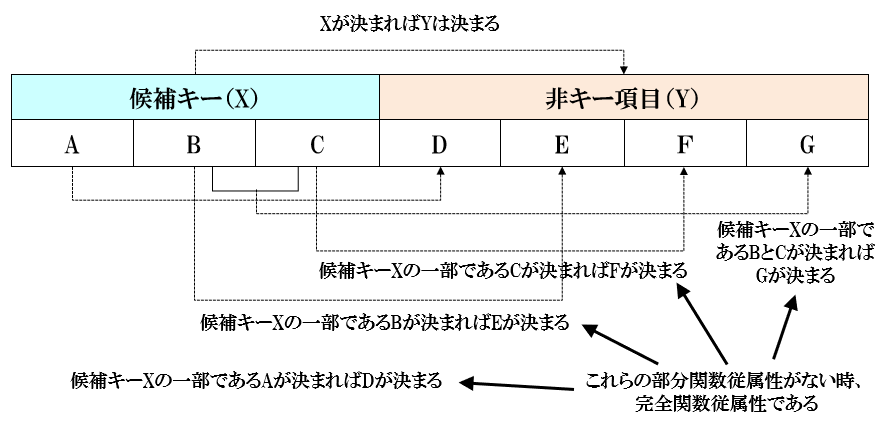
候補キーの一部に関数従属が存在することを部分関数従属性と言いいます。完全関数従属性とは、候補キーの一部に関数従属性がない状態を言います。上図のA、B、Cは候補キーXを構成する属性(項目)です。候補キーXが決まれば非キー属性(項目)Yは決まると言う関数従属性がある場合、候補キーXの一部であるA、B、C、AB、AC、BCによって非キー属性(項目)Yの属性(項目)が決まるという関数従属性がない時、完全関数従属性であると言います。
推移関数従属の意味
以下の図は推移関数従属性を表した図です

X → Y かつ Y → Z であるならば、X → Zの関数従属性がある。これを推移関数従属性と言います。 上図のA、B、Cは候補キーXを構成する属性(項目)である。候補キーXが決まれば非キー属性(項目)Yは決まると言う関数従属性があり、非キー属性(項目)Yの一部Fが決まれば同じく非キー属性(項目)Gが決まるという関数従属性がある時、 X → Y(F) かつ Y(F) → Z(G) となり、X → Z(G)の関数従属性がある。これを推移関数従属性と言います











